2011 DL12 is an outer main-belt asteroid.
I have downloaded the orbital parameters from
JPL Small-Body Database Browser:
[ show orbit diagram ]
Orbital Elements at Epoch 2458600.5 (2019-Apr-27.0) TDB
Reference: JPL 4 (heliocentric ecliptic J2000)
| Element | Value | Uncertainty (1-sigma) | Units |
| e | .3332919522378502 | 1.7048e-05 | |
| a | 3.813848977356317 | 0.00010804 | au |
| q | 2.542723806152901 | 1.7234e-05 | au |
| i | 13.48245115796516 | 0.00011571 | deg |
| node | 329.3312783932701 | 0.00010623 | deg |
| peri | 151.9591228706485 | 0.0023481 | deg |
| M | 48.29805632413862 | 0.016968 | deg |
| tp | 2458235.518528997214
(2018-Apr-27.01852900) | 0.11275 | TDB |
| period | 2720.468266449358
7.45 | 0.1156
0.0003165 | d
yr |
| n | .1323301596419123 | 5.6232e-06 | deg/d |
| Q | 5.084974148559733 | 0.00014405 | au |
|
| | Orbit Determination Parameters
Additional Information
|
I generated 100 clones trying to achieve the same nominal orbital parameters and uncertainty as calculated by JPL.
The result (achieved vs target) is shown in this table:
|
Clones | |
Target |
|
mean |
sd |
|
mean |
sd |
| q |
2.54272169 |
1.715e-05 |
|
2.54272381 |
1.723e-05 |
| e |
0.33329091 |
1.712e-05 |
|
0.33329195 |
1.705e-05 |
| i |
13.48245868 |
0.00011564 |
|
13.48245116 |
0.00011571 |
| peri |
151.95937755 |
0.00234384 |
|
151.95912287 |
0.0023481 |
| node |
329.33127117 |
0.00010601 |
|
329.33127839 |
0.00010623 |
| tp |
2458235.53032508 |
0.11307094 |
|
2458235.518529 |
0.11275 |
Backward Simulation
As shown below, I investigated what could have happened to the clones in the past going back to -100 million JD (about 280K years in the past).
As arbitrary threshold to declare that an object is likely to have a cometary origin, I set ejection distance = 100 AU
Algorithm: Bulirsch-Stoer
Non gravitational effects: not taken ito account.
Software: Mercury 6
===> reference for the package: J.E.Chambers (1999) ``A Hybrid
Symplectic Integrator that Permits Close Encounters between
Massive Bodies''. Monthly Notices of the Royal Astronomical
Society, vol 304, pp793-799.
)O+_06 Integration parameters (WARNING: Do not delete this line!!)
) Lines beginning with `)' are ignored.
)---------------------------------------------------------------------
) Important integration parameters:
)---------------------------------------------------------------------
algorithm (MVS, BS, BS2, RADAU, HYBRID etc) = BS
start time (days)= 2458200.5
stop time (days) = -1d8
output interval (days) = 100
timestep (days) = 0.05
accuracy parameter=1.d-12
...
ejection distance (AU)= 100
Simulation Results
(all analysis and plots below are done with R version 3.5.1 (R: A Language and Environment for Statistical Computing) using many libraries including library ggplot and viridis).
Going back in the past, 77 out of 100 clones seem to have a cometary origin because they entered the solar system coming from a distance greater than 100 AU.
As the simulation is backward, this plot should be read from right to left: we can see that many of the initial 100 clones are slowly "ejected" from the solar system (i.e. they entered in the solar system):
This plot show the density distribution of the arrival time in the solar system:
It seems that the most of the clones arrived in the solar sytem about 35000 years ago.
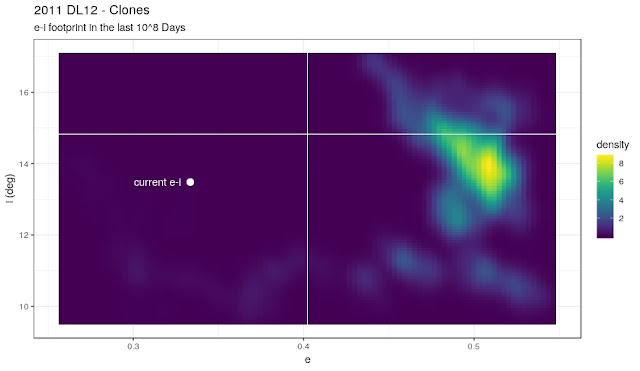
Footprint plots
If we forget the temporal dimension, we can draw some "footprint" plots that show where the clones were for most of the time:
Time plots
In the following plots, we take again into consideration the temporal dimension.
We
start defining 10 time slots.
We take the first time slot and consider the first clone: we calculate the mean (or min/max) of an orbital parameter. Thus, we have one value.
Then, we do the
same calculation for the other clones in the first time slot and we draw the resulting boxplot
showing the distribution of all values.
The number of clones contributing to each interval in written over the boxplot itself.
The process is repeated for every time slot.
minimum value of perihelium
In case of aphelium, we need to discard a couple of outliers in order to be able to see the boxplots that otherwise would be too much "compressed":
maximum value of aphelium
maximum value of eccentricity:
mean value of inclination
mean value of w
mean value of om
In the energy plot, clones with hyperbolic orbits have energy greater than 0
maximum value of energy
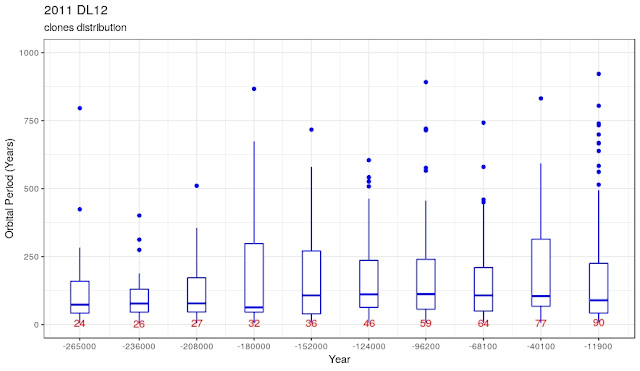
For hyperbolic clones we can show the Vinfinity while for the other we can show the orbital period (in the latter case, we discard a few outliers to better see the boxplots):
maximum value of Vinfinity
maximum value of orbital Period
Analysis of close encounters
Kind Regards,
Alessandro Odasso