Near-Earth Asteroid Delta-V

JPL maintains an interesting list: Near-Earth Asteroid Delta-V for Spacecraft Rendezvous

Let's display how Delta-V depends on perihelium q=a*(1-e)

(Graphs are done with  R package and the related ggplot function)

Neo with q <=1
Delta-V (km/s) vs q (AU)

The red line is a very rough approximation for the lower boundary of Delta-V (km/s) as a function of q (AU):

delta-v = -7.3q + 11.4 when q<=1

Neo with q> 1
Delta-V (km/s) vs q (AU)

The red line is a very rough approximation for the lower boundary of Delta-V (km/s) as a function of q (AU):

delta-v = 4.6q - 0.5 when q>1

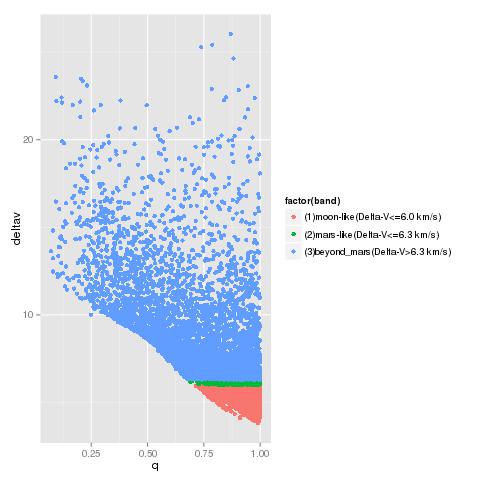
Three "bands" for Delta-V
As stated in the JPL page, for comparison, Delta-V for transferring from Low Earth Orbit to rendezvous with Moon and Mars:

• Moon: 6.0 km/s
• Mars: 6.3 km/s

Thus, we can graphically display three bands for Delta-V. I call them as follows:
1) moon-like (Delta-V <= 6.0 km/s)
2) mars-like (Delta-V <= 6.3 km/s)
3) beyond-mars (Delta-V > 6.3 km/s)

Neo with q <=1
Delta-V (km/s) vs q (AU)

Neo with q > 1

Delta-V (km/s) vs q (AU)

We can look at the neo distribution in every Delta-V band:

Neo with q <=1

Neo with q >1

Ultra-low Delta-V Neo

I often read that these neo are considered as a particular interesting target for   spacecraft rendezvous missions because very little energy is needed to reach them.

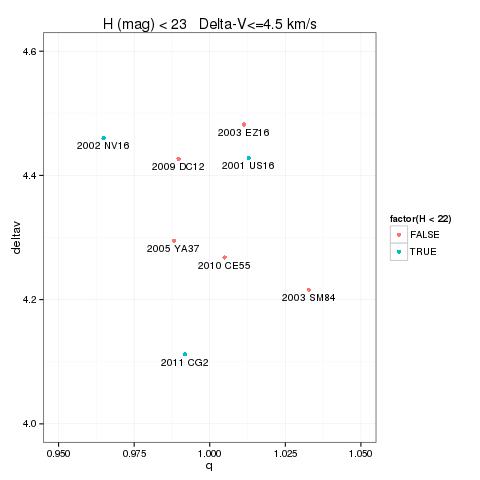
This is a graphical display for neo with Delta-V <= 4.5 km/s:

These ultra low Delta-V neo are just a tiny fraction of the neo population.
This is their proportion:

As known, one of the problems with these neo is that it is very difficult to find relative bright (and thus big) asteroids.

The graph below shows all the ultra low Delta-V asteroids with H (mag) <= 23 showing that only three neo of this group have H (mag) <= 22. They are:

Designation	Delta-V (km/s)	H (mag)
2011 CG2	4.112	21.5
2001 US16	4.428	20.2
2002 NV16	4.460	21.4

(1999 RQ36) Bennu and ("similar?") Neo

Delta-V for Bennu: 5.087 km/s
H (mag) = 20.9

See also:
http://en.wikipedia.org/wiki/101955_Bennu
http://astro.mff.cuni.cz/davok/papers/bennu_osiris_maps2015.pdf

If we give a look at asteroids having Delta-V and H at least comparable (or better) than those of asteroid Bennu, target of the OSIRIS-REx mission, we can find a few other ones.
Bennu is shown at the top-left corner of the image.

Of course, Delta-V is not the only parameter used to decide whether an asteroid is a good candidate for a sample return mission (physical characteristics, a well known orbit and an appropriate rendezvous time are certainly other fundamental aspects!). 

Once said this, I would be interested to know if some of the other asteroids shown here are candidates for similar missions.
In fact, I found an interesting link showing the earth-centric orbit view of many of these asteroids

 

Kind Regards,
Alessandro Odasso

Asteroid Spectral Type Distribution up to 1st Kirkwood gap

I would like to analyze the relation between asteroid spectral types and photometric data.

MPC has made available an interesting web service to download data from their databases.

Data Acquisition

The web service can be accessed running a powerful Python script that return a lot of asteroids' physical and orbital parameters (more than 100 columns!).

The first python query that I used to extract the list of asteroids was like this:

python mpc-fetch.py order_by semimajor_axis taxonomy_class_min A semimajor_axis_min 0 > part1.xml

This syntax allows you to get all asteroids belonging to taxonomy class A, B, C etc. without having to bother for those that are not yet classified.

The web service limits the output to 16384 asteroids so I had to look at the last xml section, I read the last semimajor_axis value and then I submitted the second query:

python mpc-fetch.py order_by semimajor_axis taxonomy_class_min A semimajor_axis_min 2.2179251 >> part2.xml

Then I repeated the process and I run:

python mpc-fetch.py order_by semimajor_axis taxonomy_class_min A semimajor_axis_min 2.2718021 >> part3.xml

... and so on, till I reached semimajor_axis about 2.5 au where I stopped: no reason to choose this value, I chose it just to limit the number of queries (although, the threshold of 2.5 au is also nice because this is the first big Kirkwood gap).

After that, I had to convert the XML file (quite big: about 131000 ateroids) in a CSV file.

I used another python utility called xml2csv as follows (for every single file):

xml2csv --input part1.xml --output part1.csv --tag property

Finally, I concatenated all CSV files together.

Data Analysis
I used a data mining package called Weka developed by the University of Waikato in New Zealand.

The distribution of asteroids is like this:

Within a set of 131072 asteroids, we can easily see the top three groups:

• Nr. of S type - 111565
• Nr. of C type - 13207 
• Nr. of E type - 5671

Let's see how we can recognize these three groups based on some physical parameters chosen among color indexes.
 

First of all I used the "Select Attribute" tool to rank the list of the most important parameters (among color indexes) that can be used to predict the taxonomy class.

This is the result:

Panstarrs parameters are on top of the list, almost all with the same average merit.

It is nice to visually show why.

Panstarrs parameter distribution
These graphs, made with the ggplot2 tool of the R package, confirm that the panstarrs parameters allow to discriminate between S-type, C-type and E-type asteroids.
In fact, every single distribution is constituted mostly of asteroids belonging to the same taxonomy class.

We can also visually display the covariance matrix as a "heatmap".
I found a very interesting link that explains how to do this:
ggplot2 : Quick correlation matrix heatmap - R software and data visualization

This is the result:

Finally, let's go back to Weka and perform:

• cluster alanysis
• logistic model

Cluster Analysis

I run a K-means clustering algorithm with K=3:

• The S-type asteroids were associated to cluster 0
• The C-type asteroids were associated to cluster 1
• The E-type asteroids were associated to cluster 2
• All different types were mainly attributed to cluster 0 with the exception of V-type that were grouped in the same clusters of E-type asteroids. Cluster 1 is entirely constituted of C-Type asteroids.

The clustering schema in this case is powerful: in fact only 0.48% of the asteroids were incorrectly clustered:

The three cluster centroids are as follows:

The Weka Logistic model
First of all, we must establish a performance boundary about what we expect to get (ZeroR model).
There are 111565 S-type asteroid in a set of 131072 asteroids: the accuracy of any "true" model must be much better that 85%.

After running the logistic model with a N=10 cross-validation, I got these results:

As expected, very good performance not only for S-type asteroids but also C-type asteroids (precision and recall = 1) and E-type asteroids (precision=0.928, recall=1) -  but failure to predict the other less numerous types.


Kind Regards,
Alessandro Odasso