Amor 2002 RN38

This NEO is listed in the page of Asteroids with Comet-Like Orbits maintained by Y. Fernandez.

It was also discussed as an object with a likely cometary origin in some papers, among which I found:

• "On Near-Earth Asteroid Study at Department of  Astronomy, Bandung Institute of Technology" by S. Siregar.
• "Assessing the physical nature of near-Earth asteroids through their dynamical histories" by Julio A. Fernández, Andrea Sosa, Tabaré Gallardo, Jorge N. Gutiérrez.

At the time I made this analysis, this Amor was last observed on November 11th, 2017 and the orbit uncertainty is 0 being based on 119 observations acquired in the last 15 years.

JPL Small-Body Database Browser:

Orbital Elements at Epoch 2458000.5 (2017-Sep-04.0) TDB
Reference: JPL 31 (heliocentric ecliptic J2000)

Element Value Uncertainty (1-sigma)   Units  e .6730769823381273 2.1793e-07 a 3.820825408551513 1.2346e-07 au q 1.249115772522818 7.9678e-07 au i 4.160437503290696 1.756e-05 deg node 296.1904517164833 0.00024613 deg peri 118.6156866423836 0.00026072 deg M 357.1006606538095 3.1062e-05 deg tp 2458022.470035828635 (2017-Sep-25.97003583) 0.00023642 JED period 2727.936248200967 7.47 0.00013222 3.62e-07 d yr n .1319678933983206 6.3964e-09 deg/d Q 6.392535044580208 2.0656e-07 au

Orbit Determination Parameters    # obs. used (total)      119      data-arc span      5568 days (15.24 yr)      first obs. used      2002-08-18      last obs. used      2017-11-15      planetary ephem.      DE431      SB-pert. ephem.      SB431-N16      condition code      0      fit RMS      .55328      data source      ORB      producer      Otto Matic      solution date      2017-Nov-16 07:18:58   Additional Information  Earth MOID = .270556 au   Jupiter MOID = .260678 au   T_jup = 2.626

I simulated 100 clones of this asteroid in the past 10^8 days trying to confirm its possible cometary origin: the goal is to determine whether some clones might have arrived from the outskirt of the solar system - arbitrary threshold: 100 AU.

Simulation approach

Mercury6 Integrator

reference:

J.E.Chambers (1999) 

A Hybrid Symplectic Integrator that Permits Close Encounters between Massive Bodies''. Monthly Notices of the Royal Astronomical Society, vol 304, pp793-799.

           Integration parameters
           ----------------------

   Algorithm: Bulirsch-Stoer (conservative systems)

   Integration start epoch:         2458000.5000000 days
   Integration stop  epoch:      -100000000.0000000
   Output interval:                     100.000
   Output precision:                 medium

   Initial timestep:                0.050 days
   Accuracy parameter:              1.0000E-12
   Central mass:                    1.0000E+00 solar masses
   J_2:                              0.0000E+00
   J_4:                              0.0000E+00
   J_6:                              0.0000E+00
   Ejection distance:               1.0000E+02 AU
   Radius of central body:          5.0000E-03 AU


Simulation Results

• 79 out of 100 clones have a cometary like orbit.
• of which: 13 came on a hyperbolic orbit (Vinfinity = 42.1219*sqrt(-0.5/a) --> the minimum absolute value for semi-major axis a was -17.46 AU -->the maximum value for Vinfinity was 7.14 km/s 
• 1 out of 100 was discarded because "hit" the sun (due to extremely high eccentricity).

The time when they entered the solar system was distributed as follows:

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
-272319 -151956  -85380 -100222  -38660    -370

In a graphical form:

The most recent arrival in the solar system could have happened a relatively short time ago compared to other asteroids with a cometary like orbit: year 370 B.C.

A look at the nominal asteroid

The nominal asteroid is one of the 79 clones with a cometary like orbit. It apparently arrived in the solar system about in year 87000 B.C 

In the following plots (made with R package ggplot2), the vertical dashed lines show a close encounter with Jupiter.

Close Approaches analysis
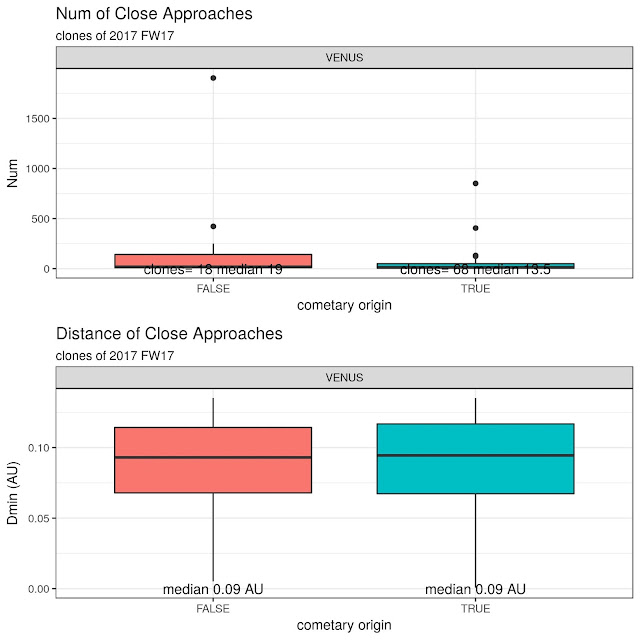
For every given planet, every clone had a certain number of close approaches so we can calculate the mean number of close approaches and the mean number of Dmin (distance of the close approach). Even better, we can print a boxplot showing the distribution of the number of close approaches and their distances.

Kind Regards,
Alessandro Odasso

Near Earth Asteroids - Low Delta-V - Frame of reference co-rotating with earth

Due to their earth like orbit, these low delta-v asteroids move slowly when seen from earth. The resulting movement is very nice.

I tried to visualize asteroids which are likely to be lunar ejecta. I also add Bennu that moves much faster but it is interesting to see how it gets "near" to the earth during the Osiris-REx mission 

All the other asteroids are sorted by Delta-V.

The last two asteroids have a very low eccentricity.

The following graphs show their movement in the next 10 years:

• Sun is at (0,0)
• Earth is at about (1,0)

Bennu
a-e-i

1.126  0.204    6.0 

 
2006RH120
a-e-i 

1.033  0.024    0.6

2012TF79
a-e-i

1.050  0.038    1.0

2009BD
a-e-i 

1.062  0.052    1.3

2014WX202
a-e-i 

1.035  0.059    0.4

1991VG
a-e-i 

1.027  0.049    1.4

2013RZ53 (maybe artificial, though not very likely: see this link)
a-e-i

1.013  0.027    2.1

2014WA366
a-e-i 

1.034  0.071    1.6

2014WU200
a-e-i 

1.027  0.072    1.3

2015JD3
a-e-i 

1.058  0.008    2.7

2014TW
a-e-i 

1.029  0.009    9.0

Kind Regards,
Alessandro Odasso

Near-Earth Asteroid Delta-V

JPL maintains an interesting list: Near-Earth Asteroid Delta-V for Spacecraft Rendezvous

Let's display how Delta-V depends on perihelium q=a*(1-e)

(Graphs are done with  R package and the related ggplot function)

Neo with q <=1
Delta-V (km/s) vs q (AU)

The red line is a very rough approximation for the lower boundary of Delta-V (km/s) as a function of q (AU):

delta-v = -7.3q + 11.4 when q<=1

Neo with q> 1
Delta-V (km/s) vs q (AU)

The red line is a very rough approximation for the lower boundary of Delta-V (km/s) as a function of q (AU):

delta-v = 4.6q - 0.5 when q>1

Three "bands" for Delta-V
As stated in the JPL page, for comparison, Delta-V for transferring from Low Earth Orbit to rendezvous with Moon and Mars:

• Moon: 6.0 km/s
• Mars: 6.3 km/s

Thus, we can graphically display three bands for Delta-V. I call them as follows:
1) moon-like (Delta-V <= 6.0 km/s)
2) mars-like (Delta-V <= 6.3 km/s)
3) beyond-mars (Delta-V > 6.3 km/s)

Neo with q <=1
Delta-V (km/s) vs q (AU)

Neo with q > 1

Delta-V (km/s) vs q (AU)

We can look at the neo distribution in every Delta-V band:

Neo with q <=1

Neo with q >1

Ultra-low Delta-V Neo

I often read that these neo are considered as a particular interesting target for   spacecraft rendezvous missions because very little energy is needed to reach them.

This is a graphical display for neo with Delta-V <= 4.5 km/s:

These ultra low Delta-V neo are just a tiny fraction of the neo population.
This is their proportion:

As known, one of the problems with these neo is that it is very difficult to find relative bright (and thus big) asteroids.

The graph below shows all the ultra low Delta-V asteroids with H (mag) <= 23 showing that only three neo of this group have H (mag) <= 22. They are:

Designation	Delta-V (km/s)	H (mag)
2011 CG2	4.112	21.5
2001 US16	4.428	20.2
2002 NV16	4.460	21.4

(1999 RQ36) Bennu and ("similar?") Neo

Delta-V for Bennu: 5.087 km/s
H (mag) = 20.9

See also:
http://en.wikipedia.org/wiki/101955_Bennu
http://astro.mff.cuni.cz/davok/papers/bennu_osiris_maps2015.pdf

If we give a look at asteroids having Delta-V and H at least comparable (or better) than those of asteroid Bennu, target of the OSIRIS-REx mission, we can find a few other ones.
Bennu is shown at the top-left corner of the image.

Of course, Delta-V is not the only parameter used to decide whether an asteroid is a good candidate for a sample return mission (physical characteristics, a well known orbit and an appropriate rendezvous time are certainly other fundamental aspects!). 

Once said this, I would be interested to know if some of the other asteroids shown here are candidates for similar missions.
In fact, I found an interesting link showing the earth-centric orbit view of many of these asteroids

 

Kind Regards,
Alessandro Odasso