In this mpml message, Sam Deen pointed out that this asteroid in not a Jupyter Troian but probably a 4-8 km size long period comet that in February 2017 achieved a perihelium low enough to start outgassing .
In this simulation, Tony Dunn confirmed that 2019 LD2 is not a Troian, Greek or Hilda but a comet that regulary makes very close passed to Jupiter and Saturn.
In fact, the object has now been given a cometary designation P/2019 LD2 (ATLAS)
For what's worth due to the uncertainty, I also tried a couple of day ago to see when the comet entered the solar system assuming a conventional distance greater than 100 au .
I simulated 100 clones in the past 280K years (Mercury6 software by John E. Chambers - Bulirsch-Stoer integration, intial timestep 0.05 days).
| Clones | Target | ||||
|---|---|---|---|---|---|
| mean | sd | mean | sd | ||
| q | 4.57802477541 | 1.671146e-05 | 4.57801992309 | 1.6782e-05 | |
| e | 0.13528015709 | 9.88572e-06 | 0.13527811197 | 9.8665e-06 | |
| i | 11.55192320685 | 1.746557e-05 | 11.55192194572 | 1.7512e-05 | |
| peri | 123.44833869054 | 0.00209362353 | 123.44893096687 | 0.0021043 | |
| node | 179.74537221523 | 0.00017704315 | 179.74536895343 | 0.00017777 | |
| tp | 2458949.96748775 | 0.01979864266 | 2458949.97292011 | 0.01993 | |
**In the meantime, the nominal parameters have been updated but I hope that this does not radically change the macroscopic behaviour.
The nominal comet entered the solar system about 32K years ago, while the most recent date for a clone to enter the solar system was about 4K years ago.
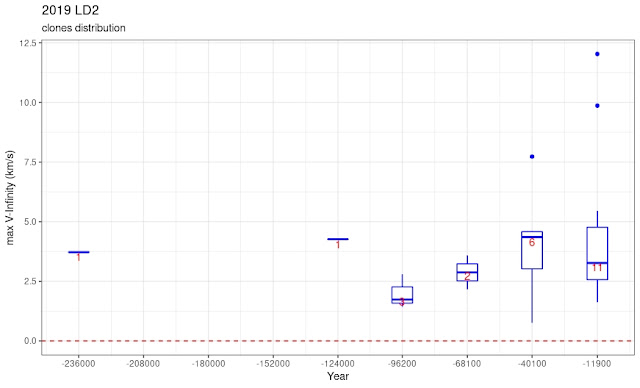
This is the overall time distribution (being a backward simulation, the clones are "ejected" from the point of view of the simulator...):
At first glance, it seemed to me that some clones entered the solar system on a hyperbolic trajectory (total energy > 0) but this is not the case.
This would be quite strange if real, many thanks to Marshall Eubanks for noting this aspect.
Looking better, we see situations like this, where you can see that the simulation does not end with the clone on a hyperbolic trajectory even if that orbit was apparently achieved in a given moment:
| Time |
a |
e |
i |
peri |
node |
long |
|
311100.5 |
11.10955 |
0.56037 |
12.7835 |
207.0631 |
179.7592 |
26.8223 |
|
311000.5 |
12.17985 |
0.599077 |
13.1885 |
206.6135 |
180.4985 |
27.112 |
|
310900.5 |
-6.12701 |
1.813375 |
2.8379 |
213.9255 |
160.4411 |
14.3666 |
|
310800.5 |
126.90366 |
0.960378 |
4.4906 |
347.4277 |
20.2166 |
7.6443 |
|
310700.5 |
58.4381 |
0.913926 |
4.4251 |
347.0157 |
20.7539 |
7.7696 |
|
310600.5 |
48.95964 |
0.897233 |
4.3941 |
346.7163 |
21.1435 |
7.8598 |
The reason why this can happen was explained by Jean Meeus:
"When one calculates the HELIOCENTRIC
orbit near the time the object is close to Jupiter, one obtains a hyperbolic
orbit, that however is meaningless because at that instant the object is
attracted more by Jupiter than by the Sun."
So in the following plots, it is safe to ignore the brief moments where the orbit has apparently a total energy > 0
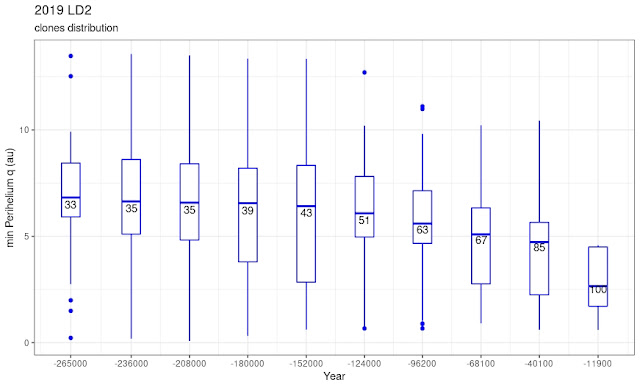
Mimimum perihelium distribution
Due to the wild uncertainty, the minimum perihelium could have been very low: in fact, about 10% of the clones could have had a close pass with Earth but not sooner than 4K years ago.
Max eccentricity distribution
(dis-regard the points with eccentricity > 1)
Kind Regards,
Alessandro Odasso