Amor - a summary plot of H vs Tisserand's parameter - Tp < 3

This post continues from the previous one.

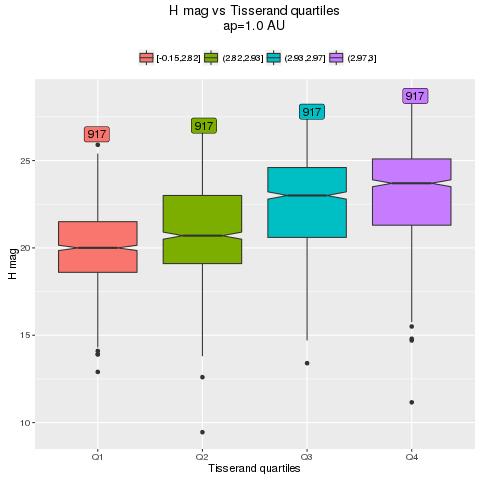
Let's take again the plot H  mag vs Tisserand's parameter with respect to Earth (ap=1 AU). 

ONLY those Amors with TEarth<3

We have already seen this plot, we just add a few labels to count them:

We have also seen that most of these Amors have also Tisserand's parameter with respect to Jupiter, Venus and Mars <  3 (actually, I refer to it as "Mars" but the exact value for which there was a relative greater correlation between H mag and Tisserand's parameter was ap = 1.65 AU).

A possible question is:how are these asteroids distributed  in the various TEarth quartiles?

For graphical purposes, I introduce the following abbreviations:

• Tm = TRUE - Tisserand's parameter with respect to Mercury < 3
• Tv = TRUE - Tisserand's parameter with respect to Venus < 3
• Tma = TRUE - Tisserand's parameter with respect to Mars (better: ap =1.65 aU) < 3

This is the result:

I do not know enough about statistic to say that the above is really significant, but I can give you my feeling.

It seems to me that:

• in TEarth quartile Q2, Q3 and Q4: those Amors having Tma < 3 (red) tend to be brighter than the others not having Tm or Tv < 3 (green)
• in TEarth quartile Q1 and Q2: those Amors having Tma < 3 and Tv < 3 (yellow) tend to be slightly darker than those having only Tma < 3 (red)
• in TEarth quartile Q1: those 79 Amors having Tm<3 (and also Tv and Tma <3) tend to be the brightest.

Below, you can see a table showing the numerosity (as also shown in the labels displayed in the plot) and the median and sd of every group:

Numerosity

> t(tapply(pe$H,list(pe$tsquartile,pe$Tm:pe$Tv:pe$Tma),length))
                  [-0.15,2.82] (2.82,2.93] (2.93,2.97] (2.97,3]
FALSE:FALSE:FALSE           NA           4          33       79
FALSE:FALSE:TRUE           213         871         884      838
FALSE:TRUE:FALSE             1           2          NA       NA
FALSE:TRUE:TRUE            624          40          NA       NA
TRUE:FALSE:FALSE            NA          NA          NA       NA
TRUE:FALSE:TRUE             NA          NA          NA       NA
TRUE:TRUE:FALSE             NA          NA          NA       NA
TRUE:TRUE:TRUE              79          NA          NA       NA

Median

> t(tapply(pe$H,list(pe$tsquartile,pe$Tm:pe$Tv:pe$Tma),median))
                  [-0.15,2.82] (2.82,2.93] (2.93,2.97] (2.97,3]
FALSE:FALSE:FALSE           NA       23.85        24.0     24.6
FALSE:FALSE:TRUE          19.7       20.60        22.9     23.6
FALSE:TRUE:FALSE          23.6       24.15          NA       NA
FALSE:TRUE:TRUE           20.1       23.10          NA       NA
TRUE:FALSE:FALSE            NA          NA          NA       NA
TRUE:FALSE:TRUE             NA          NA          NA       NA
TRUE:TRUE:FALSE             NA          NA          NA       NA
TRUE:TRUE:TRUE            19.2          NA          NA       NA

Standard deviation

> t(tapply(pe$H,list(pe$tsquartile,pe$Tm:pe$Tv:pe$Tma),sd))
                  [-0.15,2.82] (2.82,2.93] (2.93,2.97] (2.97,3]
FALSE:FALSE:FALSE           NA   0.9832238    1.984962 2.098781
FALSE:FALSE:TRUE      2.153851   2.4985271    2.592066 2.609018
FALSE:TRUE:FALSE            NA   1.2020815          NA       NA
FALSE:TRUE:TRUE       2.234240   2.1410988          NA       NA
TRUE:FALSE:FALSE            NA          NA          NA       NA
TRUE:FALSE:TRUE             NA          NA          NA       NA
TRUE:TRUE:FALSE             NA          NA          NA       NA
TRUE:TRUE:TRUE        1.967811          NA          NA       NA

Cheers,

Alessandro Odasso