As seen in the previous blog where I focused on Apollos, I am now going to do the same for Amors: look for any relation between
H mag and the
Tisserand parameter with respect to a generic body with semi-major axis
ap.

The objective is to see what happens as
ap changes in a given range.
Two simple ways to do this:
- method1: calculate the (spearman) correlation between H mag and Tp, plot the result for many values of ap.
- method2: divide the H mag and Tp range into quartiles; then, calculate the Chi-squared statistics on the resulting contingency table. Plot the result for many values of ap.
These two methods give almost the same result in the case of Apollo asteroids.
What is very strange, at least for me, is that these two methods give a different answer in the case of Amor asteroids.
In the following sections, I will describe in more detail:
- Apollo - method1
- Apollo - method2
- Amor - method1
- Amor - method2
- appendix (more graphs showing H mag vs others orbital parameters)
Apollo - method1
We calculate the spearman correlation and plot it against many values of ap. We search for minimum or maximum.
This method and the graphical result has been described in the previous blog.
Apollo - method2
I did not applied this approach in the previous blog, so I describe it in detail and I show the result.
First, we divide the H mag into quartiles (H-quartiles).
Then we calculate the Tp param for all asteroids and we divide the resulting range into quartiles (Tp-quartiles).
After that, we build a contincency table showing H-quartiles vs Tp-quartiles and, finally, we calculate the Chi-squared statistic.
The idea is just this: let's imagine for a moment that there is absolutely no relation between H mag and Tp. In such a case the Chi-squared statistic would be zero because there would be no difference between the observed values and the expected values, the latter being, by definition, the values that would be displayed when no relation exists. On the contrary, the greater the Chi-squared statistic and the greater the difference of H mag distributions between the Tp quartiles.
In order to implement all the above in
R, besides reading the orbital parameters values downloaded from
Horizons Web-Interface in a
dataframe, we need a couple of user defined functions:
The above function just implements the Tisserand formula.
func_t_h_chisq
function(ap){p$ts<-func_t(ap,p$a,p$e,p$i);p$tsquartile<-factor(cut(p$ts, fivenum(p$ts), include.lowest = T));return(chisq.test(with(p,table(tsquartile,hquartile)))$statistic)}
All asteroids parameters are in a dataframe called p.
The above function calculates the Tp values (calling the first function) for all asteroids in the dataframe p: then it calculates the quartiles (cut and fivenum instructions), the contincency table (table instruction) and the Chi-squared statistic.
In order to see the result, all we have to do is define a range for
ap (lets say
0 <= ap<=30 AU), loop calling the function and plot it:
therange<-seq(0.01,30,0.01)
plot(therange,sapply(therange,function(x)
{func_t_h_chisq(x)}),type='l',xlab="ap (tisserand
param)",ylab="H-quartiles vs Tp-quartiles - Chi-squared
statistic",main="Apollo asteroids")
The maximum correlation is found for
ap=1.03 AU
I think that this result is almost the same we achieved with method1 where we got ap = 1.01 AU.
More important: the plot seems smooth, there is a clear maximum.
Amor - method1
See previous blog for R instructions.
This is the plot showing how the correlation varies depending on the choiche of
ap:
The maximum correlation in the case of Amors is found for
ap = 2.07 AU
However, the overall behaviour is "flat" compared to the bigger variations that we saw in the case of Apollos.
In fact, the boxplot shows some differences (but not so many!) in the distribution of H depending on Tp quartiles:
Amor - method2
Following the same approach already described for Apollo asteroids, in order to see the result, all we have to do is define a range for
ap (lets say 0 <= ap<=30 AU), loop calling the function and plot
it:
therange<-seq(0.01,30,0.01)
plot(therange,sapply(therange,function(x)
{func_t_h_chisq(x)}),type='l',xlab="ap (tisserand
param)",ylab="H-quartiles vs Tp-quartiles - Chi-squared
statistic",main="Amor asteroids")
This is surprising!
There is a relative
minimum for ap = 1.29 AU
There are two relative
maxima for ap = 1.0 AU and ap = 1.94 AU
We do
not get once again the value ap=2.07 AU that was found before using the correlation method.
Let's see the corresponding boxplots to see if we have smaller differences for ap = 1.29 AU and much greater differences for ap = 1.0 AU and ap = 1.94 AU
boxplot ap=1.29 AU (minimum)
This boxplot below is done for ap=1.29 AU and, in fact, the differences of H distributions depending on different quartiles are small (with a notable exception for the 1st Tp quartile, where Amor asteroids are brighter.
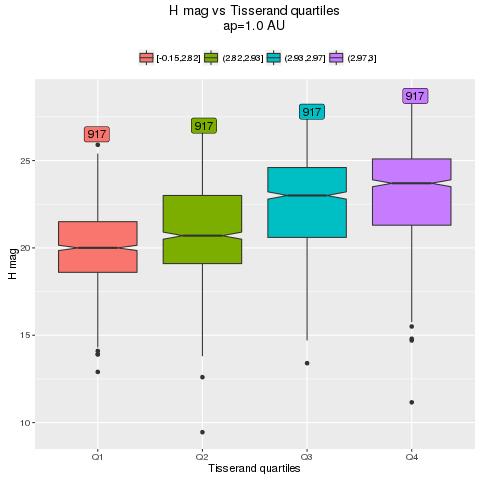
boxplot ap=1.00 AU (maximum)
This boxplot below shows what happens for ap =1 .00 AU where we can see more differences compared to the previous one (although it seems that Q1 and Q4 are more similar):
boxplot ap=1.94 AU (maximum)
This boxplot below shows what happens for ap =1 .94 AU
In this other case, there is still some difference although this time Q2 and Q3 are more similar.
The trend seems consistent with what we have see before for ap=2.07 that was found using the correlation method.
appendix
As already done for Apollo in the previous blog, let's see other graphs for Amors:
- H mag vs inclination
- H mag vs perihelium
H mag vs inclination
Higher inclined Amors are brighter
H mag vs perihelium
Amors with greater perihelium (Q4 quartile) are brighter.
This is the opposite compared with Apollo belonging to their Q4 quartile that, on the contrary, were typically darker.
Cheers,
Alessandro Odasso